| Exact & Inexact Numbers
Exact Numbers
| A 2-Part Definition: |
(Remember both parts!)
|
.
|
1.
|
Numbers obtained by counting items |
Ex: 1 potato |
|
|
|
|
|
2.
|
From an equality between two units |
|
|
in the same measuring system |
Ex: 1 yd = 3 ft |
.
Examples:
.
|
1.
|
Exact Numbers are |
8 doughnuts |
|
Numbers obtained by counting items |
2 baseballs |
|
|
|
|
|
2.
|
Exact Numbers are |
|
|
From an equality between two units |
|
|
in the same measuring measuring system |
|
|
.
U.S. System
1 foot is exactly 12 inches
1 quart is exactly 4 cups |
or
|
Metric System
1 L = 1,000 mL
1m = 100 cm |
|
.
-
The number one in any conversion is always an exact number,
whether the units are in the same system or not.
Inexact Numbers a.k.a. Measured
Numbers
The numbers you obtain when you use a measuring tool
to determine height, weight or temperature.
Examples:
.
The statue is 10.525 meters in height. It is 13.8
ºC outside.
Some measuring tools are more precise than others,
enabling a more accurate reading
.
but no matter how precise a measurement is, the
final digit in the measured number will always be an estimated digit.
Precision & Accuracy in
Measurement
Precision
The degree to which individual measurements agree
with one another.
Accuracy
The degree to which measurements taken agree with
the correct or standard value.
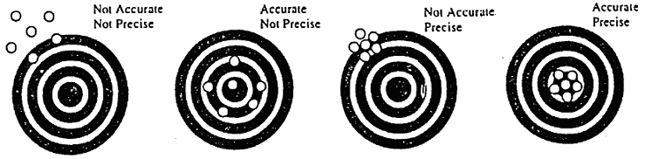
-
If measuring tools are not calibrated properly, measurements
can be precise but still be inaccurate.
Calibrating an instrument improves its accuracy.
Example: All the clocks
in the house say exactly 3:15. The time is precise.
But they are all inaccurate: The actual time is only 3:00.
Error and Percent Error in Measurement
Some quantities have an
Accepted Value
The correct value based on reliable references.
Example:
The accepted value for the boiling point of water
is 100 ºC.
Experimental Value
The value measured in a lab
Example:
You measure the boiling point of water at 99.1
ºC.
Error
The difference between the experimental value
and the accepted value.
Example:
Error = experimental value – accepted value
Error = 99.1 ºC – 100 ºC = – 0.9 ºC
Percent Error a.k.a. Relative
Error
The absolute value of the error divided by the accepted
value, multiplied by 100%.
Example:
.
|
Percent Error =
|
|
x 100% |
= 0.9% |
Significant Figures
Significant Figures
the numbers recorded in a measurement, including the
estimated digit
-
Exact numbers are not measured, do not
have a limited number of significant figures, and do not affect the
number of significant figures in a calculated answer.
-
Measurements must always be reported to the correct number
of significant figures because calculated answers often depend on the number
of significant figures in the values used in the calculation.
Examples:
You measure the mass of an object
to be 27.5 kg.
Because it is a measurement,
the number has significant figures.
The measurement 27.5 kg has three
(3) significant figures.
All the numbers in the measurement
are significant.
However, in the measurement of
0.070 kg, only two (2) of the figures are significant.
How can we determine which numbers
are significant and which are not?
Rules for Significant Figures
|
|
A number IS a
significant figure
if it is... |
|
|
Number of
significant figures |
|
|
a) not a zero |
4.5 g
|
2 |
|
|
122.35 kg
|
5 |
|
|
. |
|
|
b) a zero between nonzero digits |
205 m
|
3 |
|
|
5.082 kg
|
4 |
|
|
. |
|
|
c) a zero at the end of a
number with a decimal |
50. L
|
2 |
|
|
25.0 °C
|
3 |
|
|
16.00 g
|
4 |
|
|
. |
|
|
d) any digit in the coefficient
of a number written in
scientific notation |
5.70 x 10-3 g
|
3 |
|
. |
|
|
|
. |
|
| 2. |
A zero IS NOT
a significant figure
if it is... |
|
Number of
significant figures |
|
a) at the beginning
of a decimal number |
0.0004 lb
|
1 |
|
|
0.075
|
2 |
|
|
. |
|
|
b) used as a placeholder
in a number without a decimal |
850,000 m
|
2 |
|
|
1,250,000 g
|
3 |
|
|
. |
|
Significant Figures do not apply
to Exact Numbers.
Click HERE for a Significant
Rules Handout!
.What
is the difference between exact & measured numbers?
Practice Problems
Answer the following questions: |
|
| 1. |
Identify each of the following numbers as
measured or exact; give the number of significant figures in the measured
numbers. |
|
.
| a) 42.2 g |
b) 3 eggs |
c) 5.0 x 10-3
cm |
| . |
|
|
| d) 450,000 km |
e) 8 pencils |
f) 1,000 g = 1 kg |
|
|
|
| 2. |
For the following measured numbers, indicate
if the zeroes are significant: |
|
.
| a) 300.09 L |
b) 2.0 g |
c) 0.000 95 m |
| . |
|
|
| d) 1,000 days |
e) 1.00 x 10–9
L |
f) 7.05 x 103
kg |
|
|
|
| 3. |
State the number of significant figures in
each of the following measurements: |
|
.
| a) 0.000 35 g |
b) 2,000 m |
c) 2.004 5 L |
|
|
|
| 4. |
Can a measurement be both precise and inaccurate?
Explain. |
|
|
| 5. |
A student experimentally determines the boiling
point of water to be 98.6 ºC.
The actual boiling point of water is 100 ºC.
Calculate the error AND the percent error.
2 problems, 3 points each:
1 point for setting up the problem
correctly,
1 point for the correct answer,
1 point for the proper units
and 6 points total! |
|
|
|


